Beeldverwerking
Gesuperviseerde classificatie
Monospectrale drempelwaarde
Water: een fluitje van een cent
In sommige gevallen kan men een klasse isoleren door gewoon drempelwaarden in te voeren voor één enkele spectrale band: (monospectrale drempelmethode). Dit wordt nogal vaak gedaan voor wateroppervlakten in het nabije infrarood: alle pixels waarvan de numerieke waarde lager is dan een drempelwaarde kunnen toegewezen worden aan de klasse "water". In sommige gevallen kan een klasse van voorwerpen gedefinieerd worden door een reeks waarden (bijvoorbeeld: "alle pixels waarvoor de numerieke waarde ligt tussen 56 en 87 worden geklasseerd als loofbossen"). Deze drempelmethode wordt vaak grafisch voorgesteld op een histogram met de digitale beeldwaarden. Men bepaalt gewoonlijk de drempelwaarden op interactieve wijze.
Op het beeld van het meer van Eau d'Heure heeft men een interactieve drempelmethode toegepast in de TM4-band, voor nabij infrarood. De pixels met een waarde lager dan 42 worden in één klasse gegroepeerd, die in rode opdruk weergegeven wordt op het beeld. Deze drempelmethode is voldoende doeltreffend, ook al neemt men enkele "parasietpixels" waar. Jammer genoeg is deze methode meestal alleen bruikbaar voor de klasse "water".
Multispectrale drempelwaarden
Met blokken spelen
Als men beschikt over verschillende spectrale banden, is het ook mogelijk de drempelmethode toe te passen op verschillende spectrale banden (multispectrale drempelmethode). Om het principe van deze classificatie te visualiseren gebruikt men gewoonlijk een bijzondere vorm van histogram, scatterogram of dispersiediagram genoemd, waarmee men de verdeling van de spectrale waarden van een beeld in 2 spectrale banden tegelijk kan weergeven:
De horizontale as van de linker grafiek stelt de digitale waarden voor op de TM3-band (van 0 tot 255), en de verticale as komt overeen met waarden waargenomen in de TM2-band. Het punt aangegeven met een sterretje (*) komt dus overeen met de gecombineerde waarde 21 in de TM3-band en 23 in de TM2-band. De kleur van dit punt op het scatterogram is (bij conventie) proportioneel met het aantal pixels van het beeld die tegelijk waarde 21 in de TM3-band en waarde 23 in de TM2-band hebben. Net zoals een histogram is dit een grafiek die het aantal pixels weergeeft met een bepaalde numerieke waarde. Het gebied tussen de twee assen wordt een "spectrale ruimte" met twee dimensies genoemd. Als men een beeld wil beschrijven bestaande uit meer dan twee spectrale banden, moet men verschillende scatterogrammen gebruiken (band 1 / band 2, band 2 / band 3, band 1 / band 3). Men stelt zo vast dat het met een sterretje aangegeven punt de spectrale waarden TM2=23, TM3=21, TM4=84 heeft. De oranjerode kleur van het scatterogram op deze plaats geeft aan dat deze spectrale signatuur zeer frequent voorkomt in het beeld.
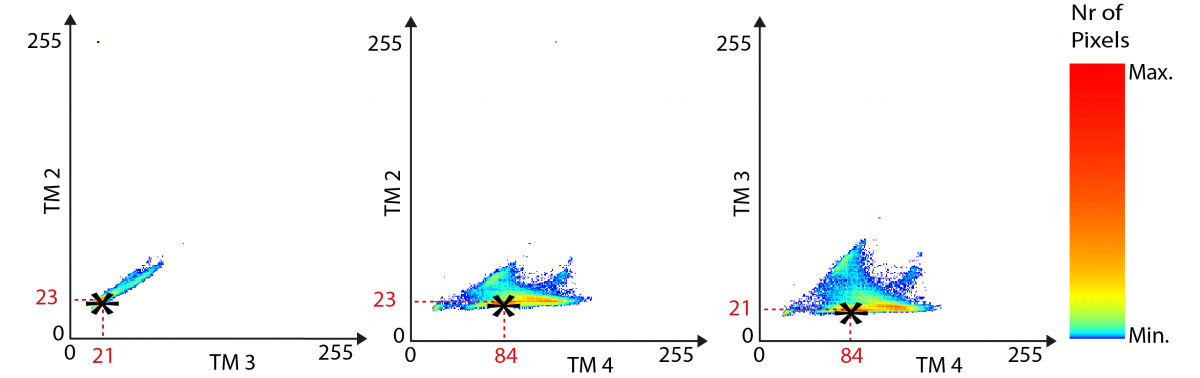
Als men gegevens analyseert met drie spectrale banden denkt men meteen aan een puntenwolk met 3 dimensies, bekeken door de drie zijden van een kubus.
De numerieke waarden van een pixel in elk van de n spectrale banden kunnen beschouwd worden als de coördinaten in een systeem met n dimensies. Een pixel komt zo overeen met een punt in een ruimte met n dimensies, soms "spectrale vector " genoemd.
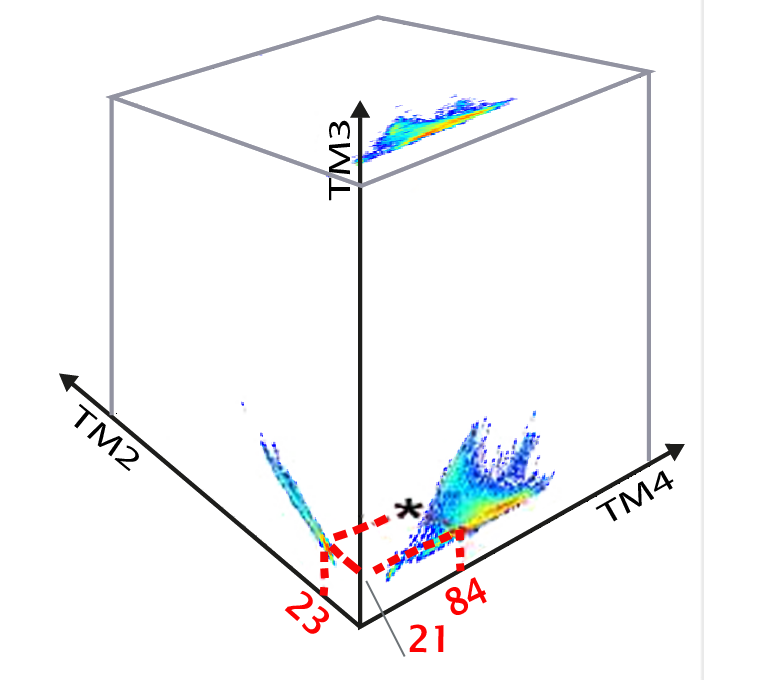Door de drempelmethode toe te passen op een spectrale band, bepaalt men de minimum- en maximumwaarden die overeenkomen met een bepaald object. Als men dit op twee spectrale banden tegelijk doet, levert het scatterogram een rechthoek op.
Als men drempels toevoegt in de derde band, vormt de puntenwolk een parallellepipedum. Als men hetzelfde doet voor elk van de klassen, krijgt men een reeks van parallellepidedumvormige "blokjes" in deze spectrale ruimte met 3 dimensies. Het spreekt vanzelf dat men ook drempelwaarden kan definiëren in spectrale ruimten met meer dan 3 dimensies, maar dan wordt de fysieke analogie abstracter.
De bepaling (voor elke klasse) van minimum- en maximumdrempels in elk van de spectrale banden is te vergelijken met een beslissingsregel. Eens die vastgelegd is, worden de spectrale waarden van elke pixel van het beeld vergeleken met de drempels bepaald in de multispectrale ruimte, en als de digitale waarde van de pixel voldoet aan alle voorwaarden voor een klasse, wordt de pixel hieraan toegewezen.
De toepassing van een dergelijke classificatie gaat via een trainingfase: de waarnemer identificeert in het beeld de gebieden waarvan hij de bedekking kent. De boven- en benedendrempels van elke klasse worden bepaald in functie van deze testpunten. Deze fase van de uitwerking van de beslissingsregel, gebaseerd op de analyse van een testpunt, wordt "gesuperviseerde classificatie" genoemd (eigenlijk kan de monospectrale drempelmethode ook beschouwd worden als een ruwe gesuperviseerde classificatie).
Minimum afstand classificatie
Bij elkaar blijven!
Het principe van de minimumafstandclassificatie ("Minimum distance classification") verschilt niet fundamenteel van de multispectrale drempelwaarde classificatie: ook hier legt men de eigenschappen van de beslissingsregel vast op basis van de spectrale eigenschappen van steekproefsgewijs gekozen gebieden of 'monsters' die representatief zijn voor de verschillende klassen van voorwerpen.
Bij de vorige methoden leverden de minimum- en maximumdrempels parallellepipedumvormige gebieden ("blokken") in de multispectrale ruimte. Bij deze methode bepaalt men het "zwaartepunt" van elk van de klassen en de spectrale vectoren die overeenkomen met pixels worden toegewezen aan de klasse van het dichtstbijzijnde zwaartepunt.
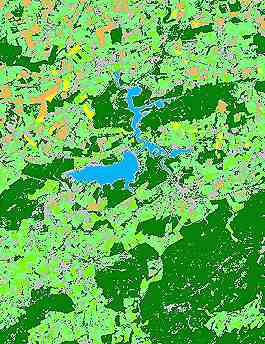
In dit voorbeeld onderscheidt men een klasse water (blauw), een type bos (donkergroen), twee graslanden (lichtgroen), en twee types gewassen (geel en oranje). Men kan geen onderscheid maken tussen de bebouwde oppervlakten, de wegen en sommige gebieden met naakte bodems (grijs).
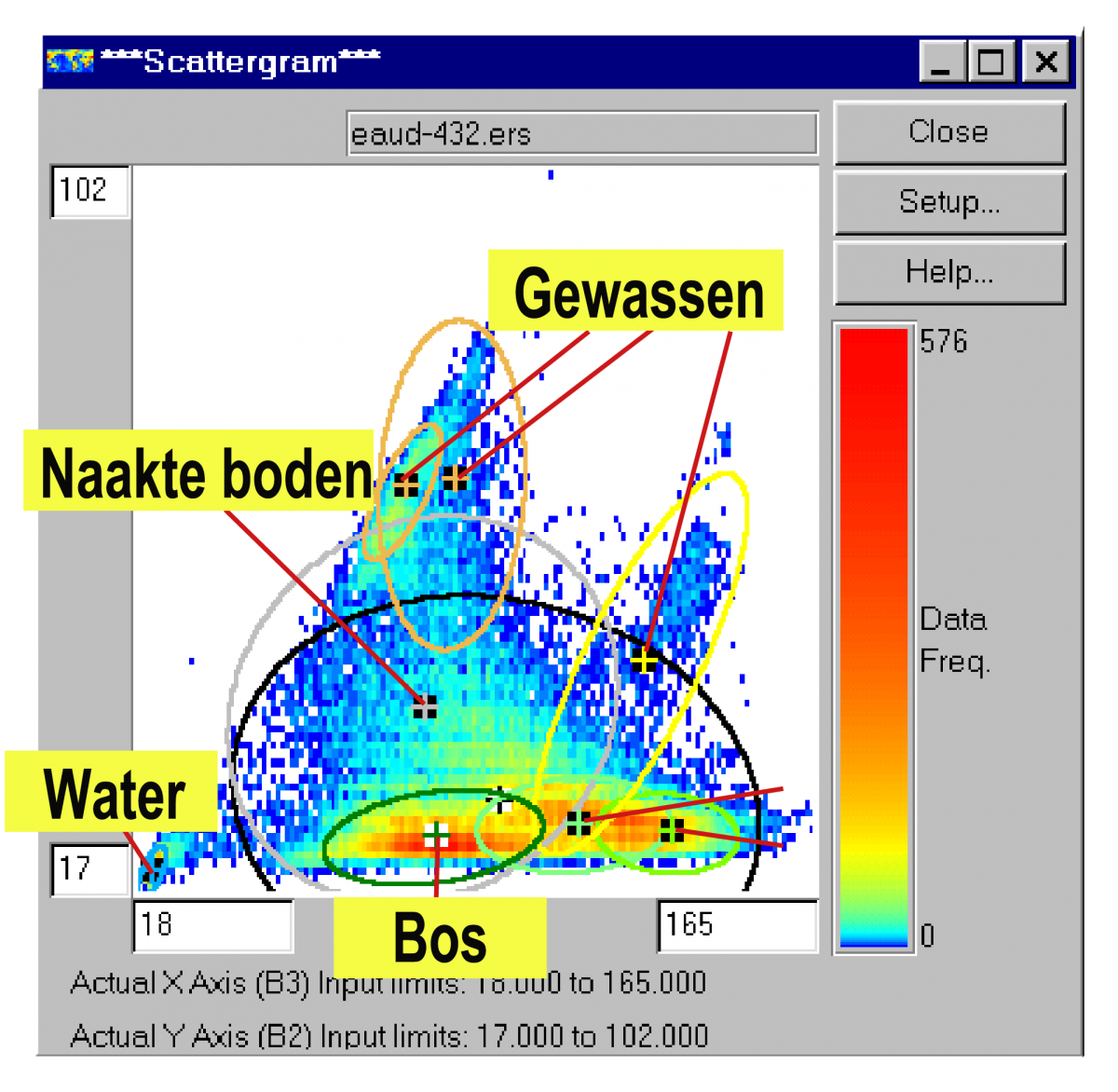
In een spectrale ruimte met 2 dimensies zijn de zones die beantwoorden aan een dergelijke beslissingsregel ellipsvormig. In een ruimte met 3 dimensies zijn het ellipsoïde volumes, enz.
Het beeld geeft een scatterogram weer met de TM4-en TM3 banden van ellipsen gevormd met deze classificatie.
Merk op dat terwijl sommige klassen zoals water, bos, grassen en sommige gewassen spectraal duidelijk gedefinieerd zijn (kleine ellipsen), andere groeperingen zeer verschillende spectrale signaturen bevatten (gewassen, naakte bodems).
Dit geeft aan dat men nieuwe "subklassen" zou moeten definiëren met homogenere spectrale eigenschappen.
Maximum waarschijnlijkheid classificatie
Dat is waarschijnlijk een bos
De classificatie via de maximum waarschijnlijkheid methode ('Maximum Likelyhood Classification') verschilt niet veel van de vorige: men gebruikt ook testpunten om de eigenschappen van klassen te definiëren. Die worden dan ook middelpunten in de multispectrale ruimte. Maar in plaats van een spectrale vector toe te wijzen aan de klasse waarvan het zwaartepunt het dichtst bij ligt, steunt men hier op een statistische analyse van de verdeling van de spectrale vectoren van het monster om gebieden met een equivalente waarschijnlijkheid rond deze middelpunten te bepalen. De waarschijnlijkheid dat een punt bij elk van de klassen hoort wordt voor elke spectrale vector berekend en de vector wordt toegewezen aan de klasse waarvoor de waarschijnlijkheid het hoogst ligt. Een aanzienlijk voordeel van deze methode is dat ze voor elke pixel, naast de klasse waaraan hij toegewezen is, een zekerheidsfactor voor die keuze geeft. Het is zo mogelijk pixels geklasseerd als "bos" met meer dan 90% zekerheid anders te verwerken dan pixels geklasseerd als "bos" met een lagere waarschijnlijkheid. Men zal dan bijvoorbeeld minder aarzelen om deze laatste pixels in een andere klasse onder te brengen bij latere verwerkingen. Toch bieden slechts weinig beeldverwerkingsprogramma’s deze interessante functie.
Post-gesuperviseerde classificatie
…of fijnregeling
Alle eerder beschreven methoden veronderstellen dat een beeldspecialist voorbeelden kan bepalen die overeenkomen met elk van de klassen die men wil identificeren. In de praktijk stelt men vast dat het meestal noodzakelijk is verschillende subklassen met licht verschillende spectrale eigenschappen te definiëren om goede resultaten te verkrijgen. Eventueel brengt men later alle pixels van deze subklassen onder in één enkele klasse. Het komt bijvoorbeeld dikwijls voor dat de spectrale eigenschappen van loofbossen sterk variëren volgens de richting van de hellingen. Als men drie subklassen bepaalt: "loofbossen op zuidelijke hellingen", "loofbossen op beschaduwde hellingen" en "loofbossen op plateau", worden de spectrale eigenschappen van de klassen preciezer onderscheiden. Dat verbetert de kwaliteit van de classificatie gevoelig, maar houdt een complexere classificatieprocedure in (er zijn meer monsters te kiezen).
Door deze logica verder te drijven, kan men een zeer groot aantal klassen definiëren, zonder zich echt te bekommeren om hun aard. Dat kan uitgevoerd worden met algoritmen die "natuurlijke" groeperingen van spectrale vectoren in de beelden herkennen. De interpretatie gebeurt dan na de classificatie, wanneer de operator een klasse moet toewijzen aan elk van de groepen pixels die in de niet-gesuperviseerde fase herkend werden. Deze aanpak biedt het voordeel dat men tijdens de identificatiefase rekening kan houden met de verdeling van de pixels die tot een zelfde groep van spectrale signaturen behoren, wat niet mogelijk is met de andere methoden.