Classification supervisée

Traitement d'images

 

Classification supervisée

Seuillage monospectral

Pour l'eau, c'est facile

Dans certains cas, il est possible d'isoler une catégorie d'objets en effectuant un simple seuillage des valeurs numériques, dans une seule bande spectrale (seuillage monospectral). C'est assez souvent le cas pour les surfaces aquatiques observées au moyen d'un capteur sensible au proche infrarouge: tous les pixels dont la valeur numérique est inférieure à une valeur seuil peuvent être affectées à la classe "eau".

Dans certains cas, une classe d'objets sera définie par une fourchette de valeurs ("tous les pixels dont la valeur numérique est comprise entre 56 et 87 sont classés comme forêt de feuillus" par exemple). Ce type de seuillage est souvent représenté graphiquement sur l'histogramme des valeurs numériques de l'image. On détermine habituellement les valeurs des seuils de manière interactive.

Sur l'image du lac de l'Eau d'Heure, on a appliqué un seuillage interactif à la bande TM4, couvrant le proche infrarouge. Les pixels dont la valeur est inférieure à la valeur 42 sont regroupés en une classe, affichée en surcharge rouge sur l'image.

Ce seuillage est assez efficace, même si on observe quelques pixels "parasites". Malheureusement, dans la plupart de cas, cette méthode n'est pratiquement utilisable que pour la classe "eau".

 

Seuillage multispectral

Une véritable mise en boîte

Si on dispose de plusieurs bandes spectrales, il est également possible d'appliquer des seuillages conjointement dans chacune des bandes spectrales (seuillage multispectral). Pour visualiser le principe de cette classification, on utilise habituellement une forme particulière d'histogrammes, appelés scattérogrammes ou diagrammes de dispersion, qui permettent d'illustrer la répartition des valeurs spectrales d'une image dans 2 bandes spectrales à la fois:

L'axe horizontal du graphe de gauche représente les valeurs numériques sur la bande TM3 (de 0 à 255), et l'axe vertical correspond aux valeurs observées dans la bande TM2. Le point indiqué par une étoile (*) correspond donc aux valeurs combinées 21 dans la bande TM3 et 23 dans la bande TM2. La couleur de ce point sur la scattérogramme est (par convention) proportionnelle au nombre de pixels de l'image qui ont à la fois la valeur 21 en bande TM3 et la valeur 23 en bande TM2. Il s'agit donc, comme un histogramme, d'un graphe qui indique le nombre de pixels ayant une valeur numérique donnée. La zone définie par ces deux axes est appelée un "espace spectral" à deux dimensions. Lorsqu'on veut décrire une image composée de plus de deux bandes spectrales, il faut utiliser plusieurs scattérogrammes (bande 1 / bande 2, bande 2 / bande 3, bande 1 / bande 3). On constate ainsi que le point indiqué par une étoile a pour valeurs spectrales TM2=23, TM3=21, TM4=84. La couleur rouge-orange du scattérogramme à cette position indique que cette signature spectrale est très fréquente dans l'image.

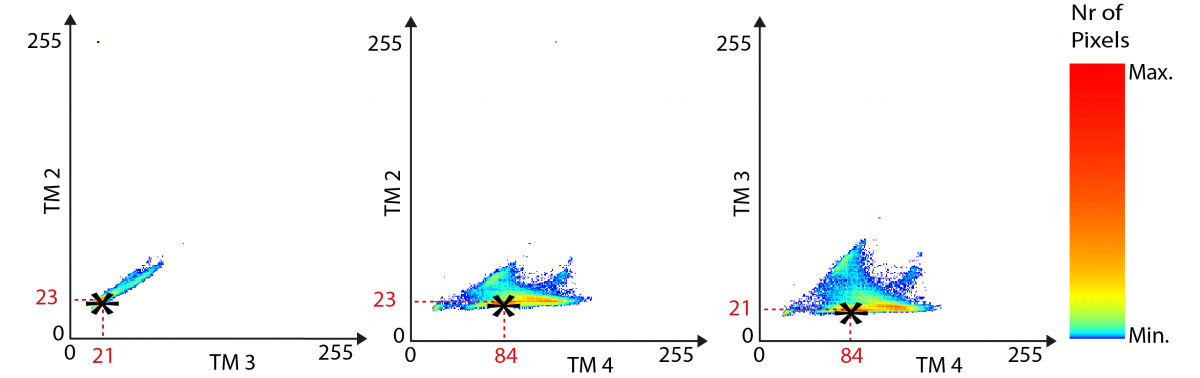
Lorsqu'on analyse des données à trois bandes spectrales, l'analogie qui vient de suite à l'esprit est celle d'un nuage de points à 3 dimensions, observé à travers les 3 faces d'un cube.
Les valeurs numériques prises par un pixel dans chacune des n bandes spectrales peuvent être vues comme les coordonnées dans un système à n dimensions. Un pixel correspond ainsi à un point dans un espace à n dimensions, parfois appelé "vecteur spectral".

En appliquant un seuillage de valeurs sur une bande spectrale, on définit des valeurs minimum et maximum correspondant à un type d'objet. La définition de seuils maximum et minimum effectuée 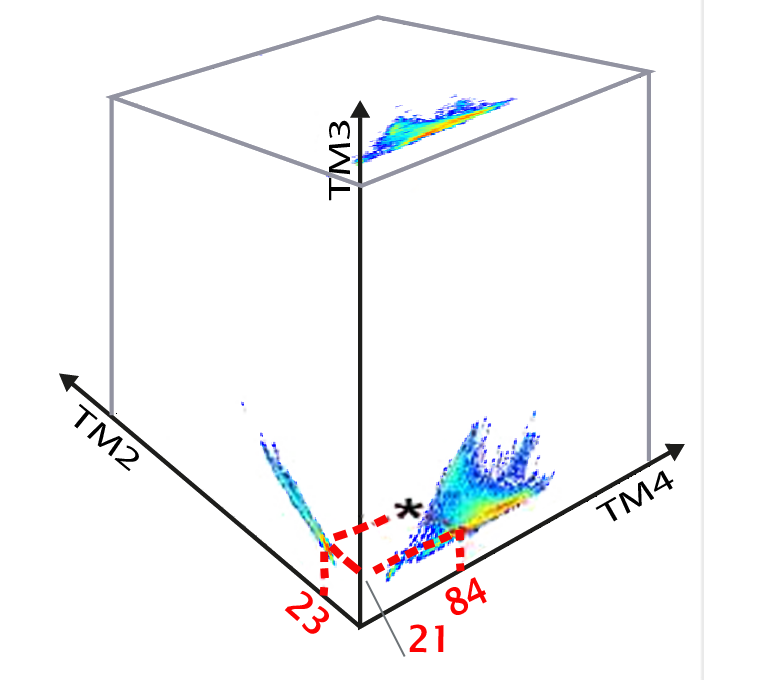conjointement sur deux bandes spectrales va définir un espace rectangulaire sur le scattérogramme correspondant. Si on ajoute des seuils sur la troisième bande, on définit une zone parallélipipédique dans le nuage de points. En faisant de même pour chacune des classes d'objets, on va définir une série de "boîtes" parallélipipédiques 
dans cet espace spectral à 3 dimensions, d'où le terme classification par boîtes. Il va de soi qu'il est aussi possible de définir des seuillages dans des espaces spectraux à plus de 3 dimensions, mais l'analogie physique devient alors plus abstraite.

La définition (pour chaque classe d'objet) des seuils minimum et maximum dans chacune des bandes spectrales s'apparente à une règle de décision. Lorsqu'elle est définie, les valeurs spectrales de chaque pixel de l'image sont comparées aux seuils définis dans l'espace multi-spectral, et si les valeurs numériques du pixel satisfont tous les tests correspondant à une classe, alors le pixel est affecté à cette classe.

La mise en œuvre d'une telle classification passe par une phase d'entrainement: l'interprète définit dans l'image des zones dont il connaît le type de couverture. Les seuils supérieurs et inférieurs de chacune des classes sont déterminés en fonction de ces zones échantillons. C'est cette phase de mise au point de la règle de décision, basée sur l'analyse d'un échantillon, qui justifie le nom de "classification supervisée" donnée à cette méthode (en fait, le seuillage mono-spectral peut également être considéré comme une forme rudimentaire de classification supervisée).

 

Classification par distance minimale

Le principe de cette classification n'est pas fondamentalement différent de la classification par boîtes: ici aussi, on définit les propriétés de la règle de décision sur base des caractéristiques spectrales de zones-échantillons choisies pour être représentatives des différentes classes d'objet. 
Les seuils minimum et maximum utilisés pour la méthode précédente définissaient des zones parallelipipédiques ("boîtes") dans l'espace multispectral. Dans cette méthode-ci, on définit plutôt le "centre de gravité" de chacune des classes, et les vecteurs spectraux correspondant aux pixels de l'image sont affectés à la classe dont le centre de gravité est le plus proche.

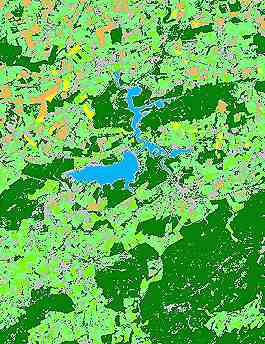
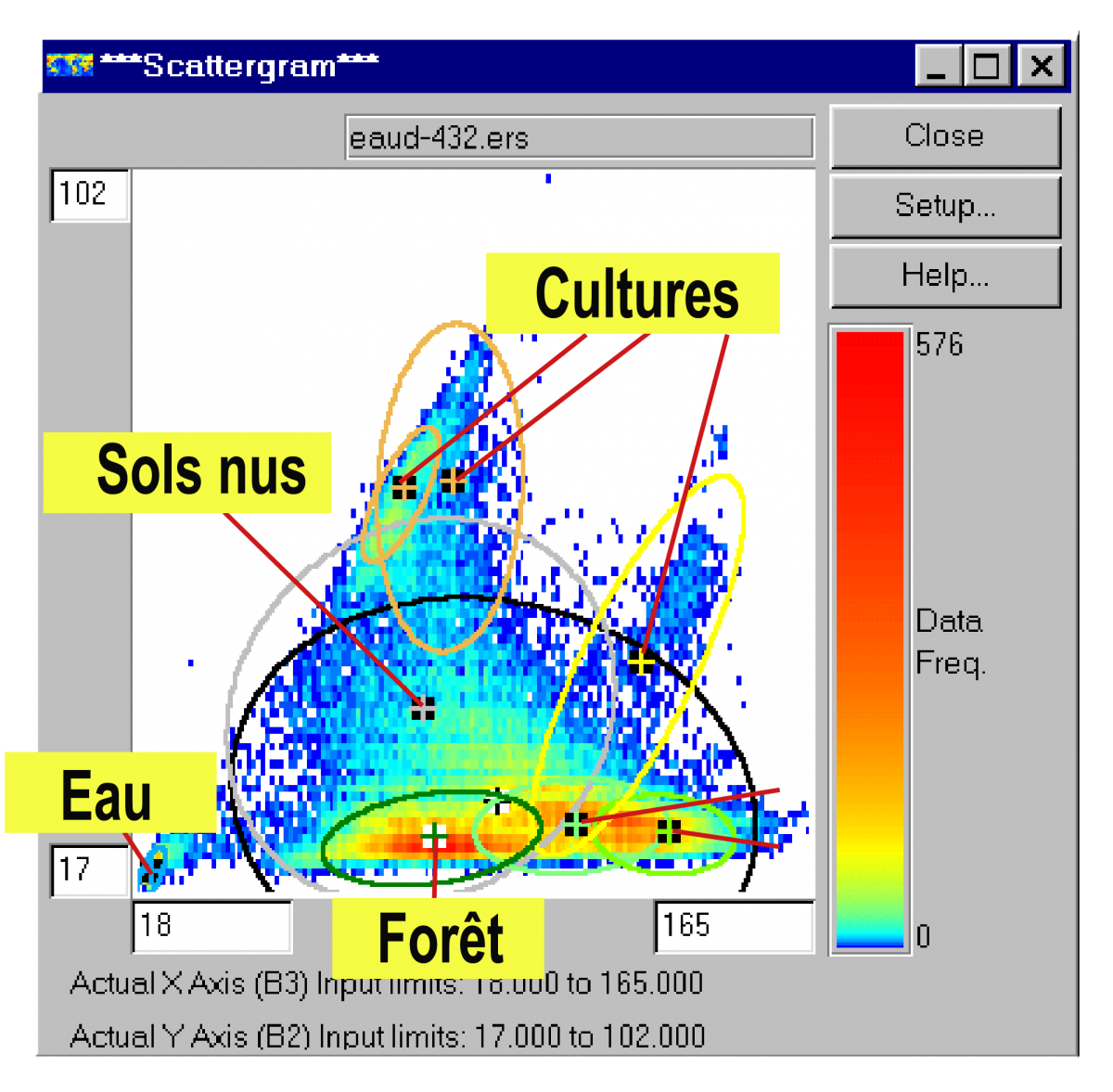
Dans cet exemple, on a distingué une classe d'eau (en bleu), un type de forêts (en vert foncé), deux types de zones herbeuses (en vert clair), et deux types de cultures (jaune et orange). Il n'est pas possible de faire la distinction entre les surfaces urbanisées, les routes et certains zones de sols nus (en gris).

Dans un espace spectral à 2 dimensions, les zones définies par une telle règle de décision sont des ellipses. Dans un espace à 3 dimensions, il s'agira de volumes ellipsoïdes, etc.

 

Classification par max. vraisemblance

Il s'agit probablement d'une forêt

La classification par maximum de vraisemblance n'est pas très différente de la précédente: on utilise également des zones-échantillon pour déterminer les caractéristiques des classes d'objets, qui deviennent également des centres dans l'espace multispectral. Par contre, au lieu d'affecter un vecteur spectral à la classe dont le centre de gravité est le plus proche, elle se base sur une analyse statistique de la distribution des vecteurs spectraux de l'échantillon pour définir des zones de probabilité équivalente autour de ces centres. La probabilité d'appartenance à chacune des classes est calculée pour chaque vecteur spectral et le vecteur est affecté à la classe pour laquelle la probabilité est la plus élevée. Un avantage considérable de cette méthode est qu'elle fournit pour chaque pixel, en plus de la classe à laquelle il a été affecté, un indice de certitude lié à ce choix. Il est ainsi possible de traiter différemment des pixels classés "forêt" avec plus de 90% de certitude, et des pixels classés "forêt" avec une faible probabilité. On hésitera par exemple moins à reclasser ces derniers pixels dans une autre classe lors de traitements ultérieurs. Pour intéressante qu'elle soit, cette possibilité n'est que très rarement exploitée par la plupart de logiciels de traitement des données de télédétection.

 

Classification post-supervisée

Toutes les méthodes décrites auparavant supposent qu'un interprète puisse définir des exemples correspondant à chacune des classes d'objets que l'on veut identifier. Dans la pratique, on constate que, pour obtenir de bons résultats, il est généralement nécessaire de définir plusieurs sous-classes d'objets, qui ont des propriétés spectrales légèrement différentes, quitte à regrouper tous les pixels classés dans ces sous-classes dans une seule catégorie après classification.

Par exemple, il arrive fréquemment que les propriétés spectrales de forêts de feuillus varient sensiblement selon l'exposition des versants. En définissant trois sous-classes "forêt de feuillus sur versant exposé au Sud", "forêt de feuillus sur versant ombragé" et "forêt de feuillus sur plateau", on précise la définition spectrale des classes, ce qui améliore sensiblement la qualité de la classification, au détriment il est vrai d'une procédure de classification plus complexe (il y a plus de zones-échantillon à sélectionner).

En poussant cette logique plus avant, on peut en arriver à définir un très grand nombre de classes, sans réellement se préoccuper de leur nature. Cela peut être fait par des algorithmes qui décèlent des groupements "naturels" de vecteurs spectraux dans les images.

L'effort d'interprétation se fait alors après la classification, quand l'opérateur devra attribuer une classe à chacun des groupes de pixels identifiés dans la phase non supervisée. Cette approche présente l'avantage de pouvoir prendre en compte lors de la phase d'identification la répartition dans l'image des pixels appartenant à un même groupe de signatures spectrales, ce que ne permettent pas les autres méthodes.