Data acquisition
Additional data
Geodesy
Geodesy is the science wich describes the size and shape of the earth.
The Earth's shape is the result of various forces. Among these forces, the most important on the planetary scale are gravity and centrifugal force.
The result of these two forces is what gives the orientation of the plumb line for any given point on Earth. That is the orientation of the local vertical. A continuous surface perpendicular to the local vertical is an equipotential surface. Among the equipotential surfaces one can define a specific one : the geoid. The geoid has a surface corresponding to mean sea level, assumed to extend at the same level under the continents. This geoid differs from the real terrestrial surface since it was modelled by different geodynamic factors.
In order to describe one's position on Earth, a person needs a simple surface which can be described mathematically. Since the 18th century, measurements have existed which prove that the Earth does not look like a perfect sphere, but rather is flattened at the poles. The appropriate mathematical description is an ellipsoid of revolution. An ellipsoid of revolution is produced by rotating an ellipse about one of its two axes. One defines the ellipsoid by describing the ellipse and the axis of rotation. The ellipsoid of the Earth has as axis of rotation the small axis of an ellipse whose precise dimensions are established at international scientific congresses. Technological progress has made it possible to define these dimensions with ever-increasing accuracy.
Depending on the country or the continent where one is working, one chooses a geodetic datum which minimises the deviation from the geoid. The geodetic data are different each time, and their centre does not coincide with the Earth's centre of mass.
As spatial measurements developed, it was necessary to define global geocentric reference systems. The most widely used system is the WGS84 (World Geodetic System 1984). This is the reference system used for the GPS.
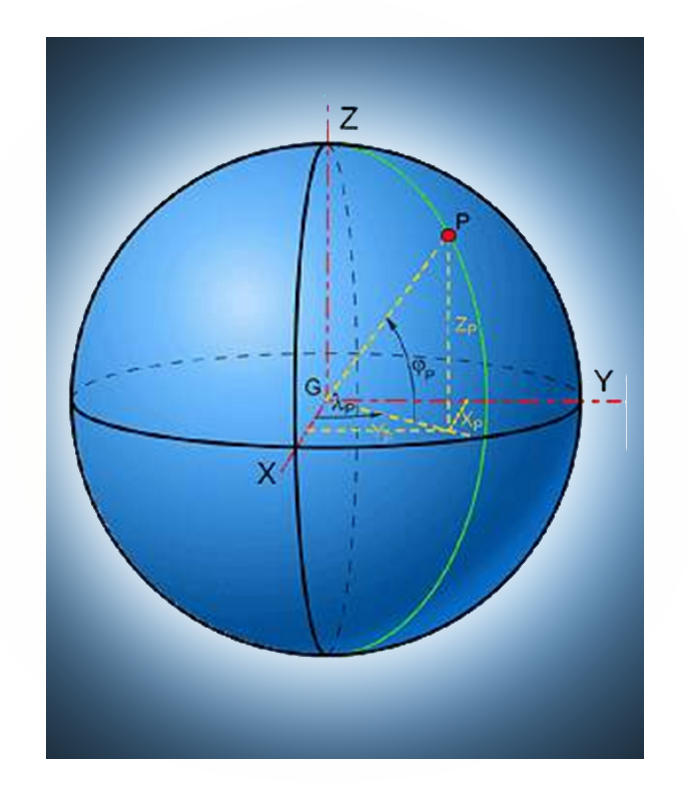
Once the datum is defined, one can describe a point on the surface of the Earth in either of two ways : by employing geocentric Cartesian co-ordinates, or by using geographical co-ordinates.
Cartographers and navigators have long since grow accustomed to locating a point with the aid of geographical co-ordinates expressed in longitude λ and latitude φ.
The longitude λ is the dihedral angle formed by the meridian of a point with the meridian of Greenwich and counted from this original meridian, positively towards the east and negatively towards the west.
The latitude φ of a point is the angle formed by the vertical of the point with the plane of the equator. Latitudes are counted from the equator, positively towards the north and negatively towards the south.
The longitude and the latitude make it possible to define a point on the ellipsoid. To situate a given point, one must also define its position with a third parameter, called the ellipsoidal height h.
One can also describe the location of a point by its geocentric Cartesian co-ordinates. Such a positioning system locates the points in X, Y and Z with the centre of the ellipsoid as origin.
Cartography
A map is a plane representation of the terrestrial surface.
Because it is impossible to develop an ellipsoid in a plane surface, one must transpose the points on the ellipsoid onto this plane surface via a projection. The points of the ellipsoid in longitude λ and latitude φ are transposed into points x and y of the map's plane surface.
x = f (λ ,φ)
y = g (λ ,φ)
This transposition inevitably introduces distortions. Many systems of projections have already been imagined, and more are still being conceived today. In principle, a projection is either conformal, equivalent or aphylactic.
A conformal projection is one which preserves the original values of the angles. An equivalent projection is one which preserves the surface relations between the ellipsoid and the plane. The transposition cannot be simultaneously conformal and equivalent. Projections which are neither conformal nor equivalent are called aphylactic. Among the latter, one can distinguish the equidistant projections, which maintain the scale in one direction.
In some transpositions of co-ordinates of the ellipsoid towards the plane, one makes use of developable surfaces. Among these transpositions, one distinguishes among cylindrical projections, conical projections and azimuthal projections, depending on whether the involute surface is a cylinder, a cone or a plane. These involute surfaces can be tangent or secant to the ellipsoid and can have different aspects. One distinguishes between direct (or normal) aspect, transverse aspect and oblique aspect. Moreover, there are an infinite number of ways to project a point of the ellipsoid onto the involute surface.
GPS
Certain basic notions of geodesy and cartography are absolutely necessary for understanding how to use the co-ordinates furnished by GPS.
The GPS (Global Positioning System) is a satellite location system set up by the DoD (Department of Defense) and the DMA (Defense Mapping Agency) of the United States. This system allows one to determine 24h a day the geographical co-ordinates of any point on Earth.
The system is composed of a network of 24 satellites orbiting at an altitude of 20 000 km in 6 different orbital planes. Each satellite emits three codes : an information code and two pseudorandom codes. The first code makes it possible to send to Earth technical information on the functioning of the satellite (calculated position of the satellite compared to fixed terrestrial stations, control parameters of the atomic clocks, etc.). The two pseudorandom codes, the C/A (COARSE/Acquisition) code and the P (Precision) code, are used for calculating position.
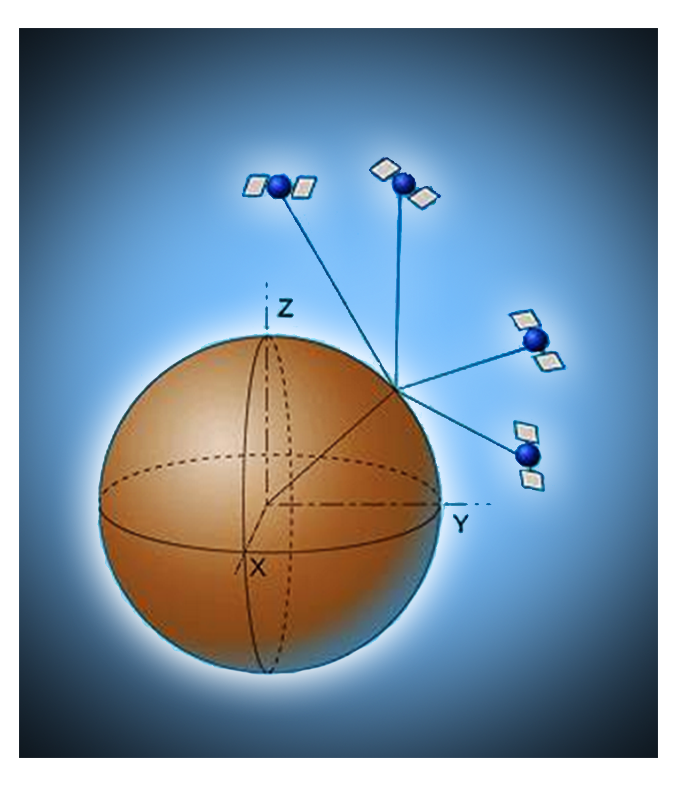
The positioning on Earth is performed by triangulating vis-à-vis the positions of the satellites. This is done using a GPS receiver. The user of the receiver measures the time interval between the emission of the signal by the satellite and the reception of the signal. This tells one the pseudodistance between the observer and the satellite. To calculate its position in geocentric co-ordinates (X, Y, Z) or in geographical co-ordinates (j, l, h), theoretically it would be enough to have the measurement of the pseudodistances between the receiver and three satellites, as well as the exact position of each satellite to know the receiver's position via triangulation. However, because the receiver does not have the same temporal precision as the atomic clocks with which each satellite is equipped, a correction must be made. One thus needs the observation of a fourth satellite to resolve the fourth variable, i.e. the error of the clock in the receiver.
The effective wavelength of Code P being substantially lower (on the order of 30m) than the wavelength of the Code C/A (300m), it goes without saying that Code P (as its very name indicates) gives more accurate information. This information is encrypted in such a way that only the military can use it. One calls this degradation of information the SA or Selective Availability. Thus, civilians cannot dispose of complete information to position themselves.
Given that it is possible to perform a measurement to a fraction of a wavelength, one can hope to attain a precision greater than 10 m for military applications and 100 m for civilian applications by the pseudodistances method.
Consultation of reference data
Remote sensing data are often combined with reference data on the ground. We can draw such data from a number of sources (aerial photos, thematic maps, field measurements, etc.) and in various forms (maps, graphs, etc.).
These data provide supplementary information allowing one to verify whether the remote sensing data are correctly interpreted. In so doing, one can also calibrate the sensors.
If one wishes to combine them with remote sensing data, they must be geo-coded, meaning that the data must be attributed a precise point in space. In the case of maps, one can read off the place in a co-ordinate system. With aerial photos one must re-project the data as necessary. With field observations, the co-ordinates are either read off from the measuring points on a map or orthophoto, or established with the aid of a GPS (Global Positioning System).